POSTS
Postgres Indexes Under the Hood
Many software engineers use database indexes every day, but few of us really understand how they work. In this post I’ll explain:
- How indexing works in Postgres using B-Trees
- What B-Trees are
- Why they are a good fit for this problem
Indexes in Postgres
Postgres actually offers 4 different kinds of indexes for different use cases. In this post I’ll be focusing on the “normal” index, the kind you get by default when you run create index. These indexes are implemented internally by Postgres using a data structure called a B-Tree. B-Trees are a generalization of binary search trees that allow nodes to have more than 2 children. The number of children per node is up to the implementer of the data structure. Databases typically have branching factors in the low thousands. Like any binary search tree you would actually use in real life, B-Trees are self balancing, giving them log(n) worst case performance for inserts, deletes, and retrieves.
B-Tree Overview
Before I dig into B-Trees in Postgres, I’ll start with a more in-depth look into B-Trees.
Image created by CyHawk - Own work based on original PNG, CC BY-SA 3.0

In binary search trees, each node has two pointers: one for all lesser values, and one for all greater values. B-Trees generalize this idea: a B-Tree node with n values will have n+1 pointers to children. Each pointer points to the subtree containing the values between its two parents. Consider the root node in the above example, which has 3 pointers.
- The first pointer, between the edge and 7, points to values less than 7
- The second pointer, between 7 and 16, points to values between 7 and 16
- The third and final pointer, between 16 and the end, points to values greater than 16.
Looking up items is straightforward: recursively follow the correct child pointer until you either find your value or a leaf. Most implementations use binary search to choose the correct child within a node. This isn’t strictly necessary in terms of big O (because the node sizes are constant), and it isn’t always beneficial in practice (unless the nodes are huge).
I’ll spare you the fairly complex description of how inserting and deletions work. It’s simple until you need to split nodes, and then it gets complicated in a hurry. The really cool part is that splitting actually inserts the median of the child into the parent. This means that splitting also rebalances the tree, making the overall implementation simpler than something like a red-black tree which requires dozens of different types of rotations.1 Consider inserting a sorted sequence of numbers into a B-Tree with 4 values (5 children) per node:
In the example above, inserting 5 causes the B-Tree to split. The split moves the median of the node into the parent (in this case there is no parent so it creates one). Selecting the median guarantees two equal sized branches.
There are two important takeaways from this section:
- B-Trees have identical big-O performance to binary search trees with log(n) search, insertion, and deletion.
- B-Trees are extremely shallow data structures. Because the branching factor is typically in the thousands, they can store millions of elements in only 2-3 layers. When used in a database, this means only 2-3 disk seeks are required to find any given item, greatly improving performance over the dozens of seeks required for a comparable on-disk binary search tree or similar data structure.
B-Trees in Postgres
Fixed Size Pages
Postgres B-Trees use 1 page of memory per node.2 Postgres pages are configurable with a default size 8KB.3 By working in entire memory pages at a time, Postgres is able to allocate memory more efficiently from the operating system. Throughout this section I’ll be using page and node interchangeably to refer to a single node in the B-Tree.
Though most theoretical B-Trees assume a fixed number of keys per node, Postgres nodes have a fixed amount of bytes. The use of fixed-size pages means that the branching factor depends on the size of each individual tuple stored in the index. If you have variable-size data, each node in your index will actually have a different number of children! Typical branching factors will be between a few hundred to a few thousand items per page. A couple interesting bits fall out of this:
- Smaller index keys can perform better than larger index keys by a small margin since they will allow a higher branching factor
- When inserting into a B-Tree, nodes must periodically be split. Normally, a node is split based on the number of items in each bucket. In Postgres, nodes are split to yield an equal number of bytes in the resulting children.
- When I was reading the Postgres source, I kept running into
ifdefsabout something calledTOAST. It turns out that Really Large (~2600 byte) keys cannot be stored in Postgres indexes.4 In the database tables themselves, Postgres uses ahackstrategy called The Oversized Attribute Storage Technique to split out the data into multiple pages.
Concurrency
Like many inventions of theoretical computer science, B-Trees require some modifications to be efficient in practice.5 Postgres uses a flavor of B-Trees outlined in Lehman and Yao’s 1981 paper. From the Postgres B-Tree readme:
Compared to a classic B-tree, L&Y adds a right-link pointer to each page, to the page’s right sibling. It also adds a “high key” to each page, which is an upper bound on the keys that are allowed on that page. These two additions make it possible detect a concurrent page split, which allows the tree to be searched without holding any read locks (except to keep a single page from being modified while reading it).
In a traditional B-Tree implementation, there is a race between getting the pointer to a child based on its expected range and the child being split by another process. A demonstrative figure from Lehman and Yao’s paper:
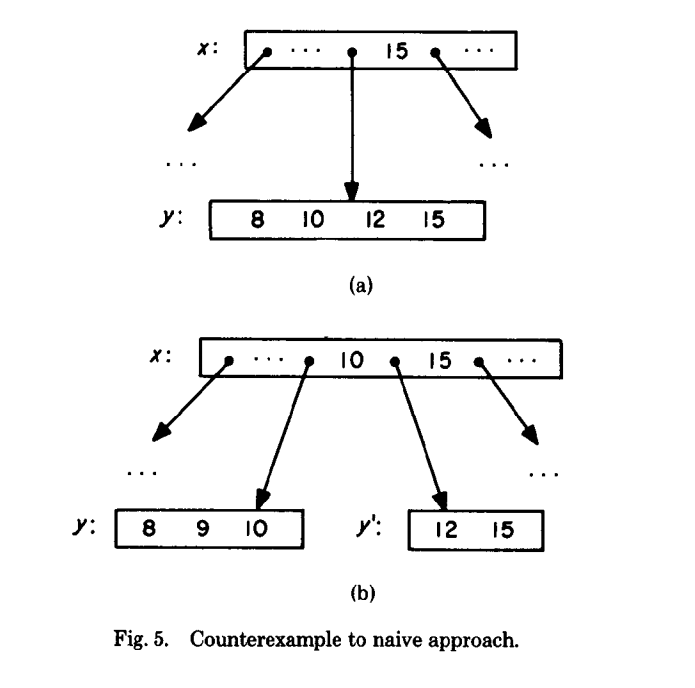
# This is not how it works in postgres. This demonstrates the problem:
"Thread A, searching for 15" | "Thread B, inserting 9"
| node2 = read(x);
node = read(x); |
"Examine node, 15 lies in y" | "Examine node2, 9 belongs in y"
| node2 = y;
| # 9 does not fit in y
| # Split y into (8,9,10) and (12,15)
| y = (8,9,10); y_prime = (12,15)
| x.add_pointer(y_prime)
|
"y now points to (8,9,10)!" |
node = read(y) |
"15 not found in y!" |The “high-key” pointer allows readers to detect that this split has occurred: If you’re looking for a value greater than the high key, you must follow the right-link! The right link allows the reader to traverse directly to the newly split node where the key now resides.
This means that readers and writers can operate concurrently, except when the writer is modifying the same node that the reader wants to read. Readers and writers acquire read-write locks, but only when actively reading or writing to a specific page. In practice, it means that as long as you aren’t reading and writing from keys that fall within the same page, you shouldn’t run into concurrency issues. It is probably worth keeping in mind that a key that is being constantly modified will slow reads and writes for keys that fall into the same node. However, since these locks are held for a much shorter duration than the user-visible Postgres locking constructs, it’s probably not worth your time worrying about it unless you see it in practice.
Multi-transaction concurrency is handled by keeping multiple copies of the data in the index. Each value in the index is associated with its transaction id. In the case of “read committed” consistency, when a transaction is searching for data in the index, it is looking for index entries with a value less than or equal the maximum committed transaction at the time the transaction started.6 In certain cases, it can detect that a simultaneous action will conflict and preemptively halt.
Alternative Indexing Strategies
A B-Tree isn’t the only way to implement a database index.
- Databases like CockroachDB that use a sorted key-value store as a storage engine usually opt to just store a copy of the table sorted by the search key instead rather than building a B-Tree index. These sorts of databases typically maintain this sorted copy of the table with a datastructure called a Log Structured Merge Tree.
- Postgres supports “hash indexes”, which utilize pages in a flat structure and address the data using hash codes. There is some cleverness to minimize moving data around when resizing. More details can be found here. They are theoretically slightly faster but they had some major deficiencies until Postgres 10 where they’re now apparently ready for prime time!
- As of 2014, SQL Server supports columnstore indexes. Since the storage is column rather than row oriented, it offers good performance on tables with large numbers of columns. Thanks to James Anderson to bringing this to my attention.
- Many databases use a variant of B-Trees called B+ Trees (Bee-Plus Trees). Rather than storing data in the nodes, all data is stored in the leaves.
B-Trees, however, are the most popular. In my brief survey of a few mainstream databases, all used B-Trees as the primary index data structure.
Do you know of a mainstream database using an alternate strategy? Please let me know so I can include it here!
In Conclusion
Hopefully this post helps to demystify what’s going on under the hood when you create and use a database index. If you ever find yourself spelunking through the Postgres source like I did for this post, the source code browser is incredibly helpful. It allows you to jump to the definitions of methods and variables, as if you were in an IDE. If there’s an area of index you wish I covered, let me know – I might write a post about it!
Want to get emailed about new blog posts?
Do you want to hire me? I’m available for engagements from 1 week to a few months. Hire me!
- Red black trees are nearly isomorphic to a B-Tree of order 4! In practice, however, red black trees will be more efficient for small amounts of data. https://en.wikipedia.org/wiki/Red%E2%80%93black_tree#Analogy_to_B-trees_of_order_4 [return]
- Postgres does not literally use OS pages directly, but they serve a similar purpose, so they are also referred to as pages. [return]
- The default blocksize of 8KB is mentioned in passing here. In the code its a bit hard to chase down because it’s configured when Postgres is being compiled. [return]
- Each node must be able to have 3 children, 8KB/3 ~= 2600B Source [return]
- I’m looking at you, Paxos [return]
- https://momjian.us/main/writings/pgsql/internalpics.pdf, slide 59-62 [return]
